Introduction
A Binary Indexed Tree or a Fenwick Tree is a data structure that supports time processing a range sum query and updating a value.
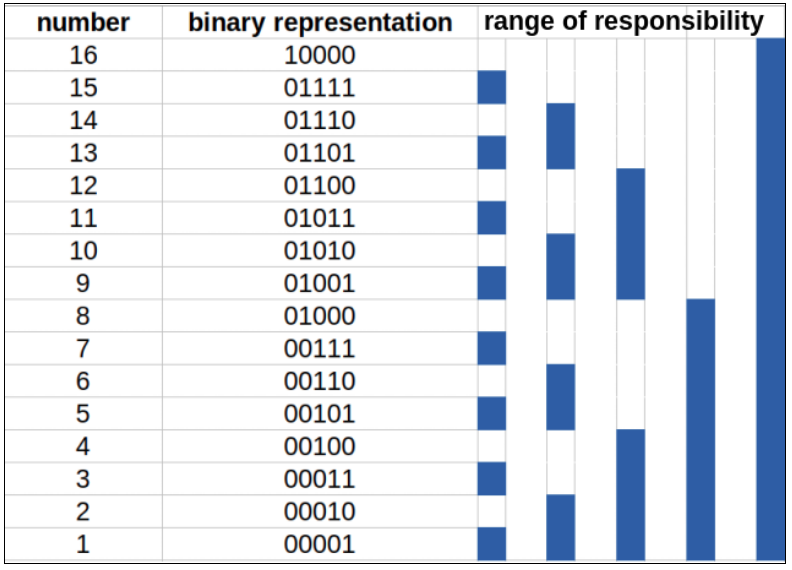
Range of Responsibility
In a Fenwick tree, a certain cell is responsible for other cells as well. The position of the first non-zero bit from right in the binary representation of the index of the cell determines the range of responsibility of that cell below itself. Let’s call this position RSB(rightmost set bit). The RSB can be found by x & (-x). Also, note that the positions from the right are one-based. The range of responsibility is 2 ^ (RSB - 1).
Let’s say we have an array
index = [1, 2, 3, 4, 5, 6, 7, 8]
array = [1, 3, 4, 8, 6, 1, 4, 2]
Let’s examine each index and its range of responsibility:
-
1 (0001): Responsible for 1 value- Only responsible for itself
- Range:
[1, 1]
-
2 (0010): Responsible for 2 values- Covers elements 1-2
- Range:
[1, 2]
-
3 (0011): Responsible for 1 value- Only responsible for itself
- Range:
[3, 3]
-
4 (0100): Responsible for 4 values- Covers elements 1-4
- Range:
[1, 4]
-
5 (0101): Responsible for 1 value- Only responsible for itself
- Range:
[5, 5]
-
6 (0110): Responsible for 2 values- Covers elements 5-6
- Range:
[5, 6]
-
7 (0111): Responsible for 1 value- Only responsible for itself
- Range:
[7, 7]
-
8 (1000): Responsible for 8 values- Covers all elements 1-8
- Range:
[1, 8]
Implementation
A BIT is usually represented as an array (1-indexed).
class BIT:
def __init__(self, arr: List[int]):
self.stree = [0] * (len(arr) + 1)
for i, x in enumerate(arr):
self.change(i + 1, x)
def change(self, i, x):
while i < len(self.stree):
self.stree[i] += x
i += i & (-i)
def query(self, i):
s = 0
while i >= 1:
s += self.stree[i]
i -= i & (-i)
return sComplexity
- Time complexity: for both query and modify operations.
- Space complexity:
Note
While Fenwick Tree does not support arbitrary range updating/querying value for min/max operations, it does support prefix min/max query.